Não foi possível enviar o arquivo. Será algum problema com as permissões?
Tabela de conteúdos
Histórico das aulas
No quadro abaixo será anotado o conteúdo dado em cada aula do curso. É indicado material para leitura correspondente ao conteúdo da aula nas referências bibliográficas básicas do curso:
- M & L: MAGALHÃES, M.N.; LIMA, A.C.P. Noções de Probabilidade e Estatística. IME/SP. Editora EDUSP.
- B & M: BUSSAB, W.O. & MORETTIN, P.A. Estatística Básica. 5a Edição, Editora Saraiva
| Leitura Recomendada | Exercícios Recomendados | ||||||
|---|---|---|---|---|---|---|---|
| Data | Local | Conteúdo | M & L | B & M | M & L | B & M | |
| 31/07 | PC-01 | Informações gerais sobre o curso e disciplina. Uma discussão sobre o uso de estatística e os tópicos contemplados no curso | Cap.1 | Cap.1 Sec.1.1 | — | — | |
| 02/08 | PC-01 | Introdução a probabilidades. | Cap.2 | Cap.5 | Cap.2: S2.1: 1, 3, 5; S2.2: 1, 3, 6 | Cap.5: 1, 2, 3, 5, 11, 14, 15, 18, 20 | |
| 07/08 | PC-01 | Probabilidades, propriedades, eventos soma, probabilidade condicional. Teorema de Bayes | Cap.2 | Cap.5 | Cap.2: S2.3: 2, 4, 7, 8, 11, 13, 21, 22, 28 1) | Cap.5: 23, 24, 26, 33, 34, 37, 38, 40, 41 | |
| 09/08 | PC-01 | Distribuições discreta de probabilidades: binomial, Poisson, geométrica, binomial negativa, hipergeométrica e uniforme | Cap.3 | Cap.6 | Cap.3: Sec. 3.2: 1 a 7, Sec.3.3: 1 a 6 | Cap.6: 20, 22, 23, 24 2) | |
| 14/08 | PC-01 | V.A. Discretas: definições, função de probabilidade, esperança e variância | Cap.3 | Cap.6 | Cap.3: Sec.3.1: 1, 2, 3, 5 | Cap.6: 1, 2, 3, 4, 7, 8, 9, 10, 13, 17 | |
| 16/08 | PC-01 | V.A. Discretas: função de distribuição acumulada, quantis, o processo de Poisson | Cap.3 3) | Cap.6 | Cap.3: Sec 3.4: 1, 3, 4, 5, 6, 8, 9, 11, 16, 20, 21, 27 | Cap.6: 29, 30, 32, 33, 37, 38, 39 | |
| 21/08 | — | Não haverá aula. Reposição extendendo horários das aulas dos dias 28 e 30 | — | — | — | — | |
| 23/08 | — | Não houve aula. Reposição no dia 03/09 | — | — | — | — | |
| 28/08 | PC-01 | Revisão de probabilidades | — | — | — | — | |
| 30/08 | PC-01 | Variáveis aleatórias contínuas: definição, propriedades, esperança, variância, distribuição uniforme, exponencial e normal | Cap.6 | Cap.7 Sec. 7.1 a 7.4 | Sec6.1: 1, 2, 5, Sec.6.2: 2, 5, 8 Sec.6.3: 3, 4, 8, 18, 23, 29, 33 | Cap.7: 2, 8, 9, 17, 19, 21, 24, 36 | |
| 03/09 | LABEST | Aula de dúvidas e exercícios | — | — | — | — | |
| 04/09 | PC-01 | Prova 1 | — | — | — | — | |
| 06/09 | — | Não haverá aula | — | — | — | — | |
| 11/09 | PC-01 | Demonstração do programa/linguagem R | — | — | — | — | |
| 13/09 | — | Não haverá aula – paralização nacional docente | — | — | — | — | |
| 18/09 | PC-01 | Introdução à a análise descritiva e exploratória:papel da estatística descritiva, tipos de variáveis, tabelas de frequência, gráficos:barra, setores, histograma e boxplot | Cap.1: Sec. 1.1,1.2 e 1.3 | Cap.2:Sec. 2.1,2.2 e 2.3 | Cap.1 Sec 1.2: 1 a 5 | Sec2.6:9,10,12,16 | |
| 20/09 | PC-01 | Regras para construção de histogramas, medidas-resumo, medidas de posição (média, mediana e moda), medidas de variabilidade (baseadas em desvios e amplitude interquartil) | Cap.1 | Cap.3 | Cap.1 Sec 1.4:1, 2, 4, 5, 7, 9, 10, 12, 13, 14 | Cap.3: 1,2,3,4,5,6, 14,15,16 | |
| 25/09 | — | Não haverá aula devido a viagem do professor - reposição a ser anunciada | — | — | — | — | |
| 27/09 | PC-01 | Estatística descritiva - o papel de estatística descritiva, relação com probabilidades | — | — | — | — | |
| 02/09 | PC-01 | Estatística descritiva: mais sobre tipos de variáveis e resumos adequados de dados, exemplos de aplicação, diagrama ramo e folhas. Introdução à descrição bivariada: diagramas de dispersão e coeficientes de correlação | ver B&M, Cap.4 | Cap.2: Sec 2.4 e Cap.4: Sec:4.5 | — | Cap.2: 4, 6, Cap.4: 1, 2, 4, 6, 9 | |
| 04/09 | PC-01 | Estatística descritiva bivariada: relações entre variáveis qualitativas e quantitativas, descrição envolvendo variáveis qualitativas, descrições multidimensionais e variáveis de confundimento | ver B&M, Cap.4 | Cap.4 | — | Cap.4: 11, 13, 18, 19, 20, 22, 26, 29, 30 | |
| 09/10 | PC-01 | Exercícios sobre estatística descritiva | — | — | — | — | |
| 11/10 | PC-01 | Dúvidas e Exemplos de análises | — | — | — | — | |
| 16/10 | PC-01 | Prova 2 | — | — | — | — | |
| 18/10 | PC-01 | Não houve aula por solicitação dos alunos – manifestação REUNI | — | — | — | — | |
| 23/10 | PC-01 | Inferência: introdução, objetivos, amostragem, amostras probabilisticas, amostra aleatória simples. Parâmetros, estimadores e estimativas. Estimação por ponto e por intervalo. Exemplo: inferência sobre uma proporção populacional. Ilustrações computacionais (ver código abaixo) e simulação | Cap. 7 | Cap.10 Sec 10.1 a 10.7 e 10.9 | Sec. 7.3: 6, Sec. 7.4: 5 | Cap.10: 1, 11, 12, 13 | |
| 25/10 | PC-01 | Inferência estatística: exemplos e inferência sobre outros parâmetros | Cap. 7 | Cap.10 Sec 10.1 a 10.7 e 10.9 | — | Cap.10: 17, 18 , 27 | |
| 30/10 | PC-01 | Parâmetros, estimadores e estimativas. Propriedades dos estimadores: consistência, não tendenciosidade, eficiência. Métodos de estimação: mínimos quadrados e máxima verossimilhança | Cap. 7 | Cap.10 Sec 10.1 a 10.7 e 10.9 | — | — | |
| 01/11 | PC-01 | Distribuição amostral da média. Teorema Central do Limite. Exemplos e exercícios | Cap. 7 | Cap.10 | Sec. 7.3: 4, 5, 7. Sec 7.5: 9, 10, 11, 12, 14, 15, 16, 17, 18, 22, 26, 27 | Cap. 10: 7, 8, 9, 10, 21, 22, 24, 25, 28 | |
| 06/11 | PC-01 | Intervalos de confiança para variância, média e proporções. Intervalos para diferença de médias. Intervalos uni e bilaterais. Idéias iniciais de testes de hipóteses | Cap 7 | Cap 10 | |||
| 08/11 | PC-01 | Testes de hipótese. Conceitos básicos, tipos de erro (I e II), passos de um teste de hipóteses, exemplos para distribuição normal. Valor descritivo (p-valor) | Cap 8 | Cap. 12 | Cap 8: Sec 8.1: 1 a 4, Sec 8.2: 2, 4, 5 Sec 8.3: 1, 2, 3, 4 Sec 8.4: 1, 3 | Cap 12: 1, 2, 56, 7, 8, 9, 21, 22, 23, 24 | |
| 13/11 | PC-01 | Resolução comentada dos exercícios 4, 5 e 6 da Seção 7.3 de M.& L. sobre Distribuição Amostral e Teorema Central do Limite. Introdução ao Dimensionamento de Amostra e construção analítica de intervalos de confiança | Cap 7 | Cap 10 | — | — | |
| 15/11 | PC-01 | Feriado | — | — | — | — | |
| 20/11 | PC-01 | Mais sobre testes de hipótese: testes sobre uma ou duas variâncias de distribuição(ões) normal(ais). Comparação de duas médias. Tópicos comentados: Comparação de mais de duas médias (análise de variância), ajusta de curvas, regressão e correlação) | Cap 8 e Cap. 9 | Cap 12 e Cap 13 | Sec 8.5: 1, 4, 5, 6, Sec 8.6: 2, 5, 7, 13, 21, 22, 28, 33, 37; Sec 9.2: 1, 2, 3, 5; Seção 9.3: 2, 4; Seção 9.6: 1, 2, 3, 4, 6, 10, 12 | Cap 13: 3, 4, 7, 9, 22, 30, 33. Cap 14:: 13, 14, 19 | |
| 27/11 | PC-01 | Tópicos diversos. Exercícios e dúvidas em preparação para a prova | Cap. 7, 8 e 9 | Cap. 10 a 14 | — | — | |
| 29/11 | PC-01 | 3a Prova | Cap. 7, 8 e 9 | Cap. 10 a 14 | — | — | |
Links
Ilustrações
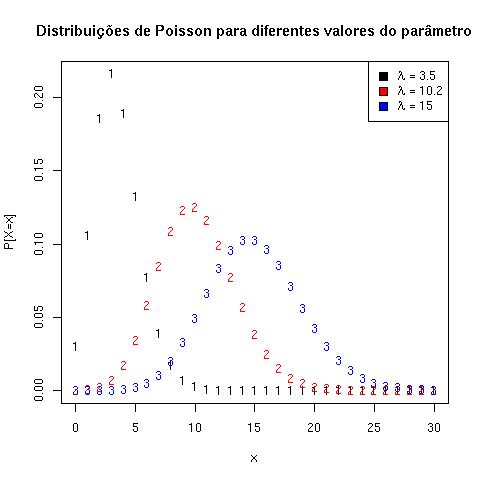
- Distribuições de Poisson com diferentes valores do parâmetro
x <- 0:30
d1 <- dpois(x, lambda=3.5)
d2 <- dpois(x, lambda=10.2)
d3 <- dpois(x, lambda=15)
jpeg("poisson.jpg")
matplot(x, cbind(d1,d2,d3), col=c(1,2,4), ylab="P[X=x]")
legend("topright", c(expression(lambda==3.5), expression(lambda==10.2), expression(lambda==15)),fill=c(1,2,4))
title("Distribuições de Poisson para diferentes valores do parâmetro")
dev.off()
- Comandos digitados na aula de 24/10/2007
## simulando de uma Bernoulli p <- 0.53 runif(1) runif(1) runif(1) runif(1) x <- runif(1) ifelse(x < 0.47, 0, 1) x x <- runif(1) ifelse(x < 0.47, 0, 1) x ## simulando 2000 respostas 0/1 am1 <- ifelse(runif(2000) < 0.47, 0, 1) am1 ## proposção estimada mean(am1) ## outra amostra am2 <- ifelse(runif(2000) < 0.47, 0, 1) mean(am2) ## .. e ainda duas outras amostras... am3 <- ifelse(runif(2000) < 0.47, 0, 1) mean(am3) am4 <- ifelse(runif(2000) < 0.47, 0, 1) mean(am4) ## simulando agora 5000 amostras de tamanho 2000 cada ams <- sapply(1:5000, function(iii) ifelse(runif(2000) < 0.47, 0, 1)) dim(ams) ams[1:20, 1:10] ## obtendo as 5000 estimativas e a sua distribuição amostral aproximada pest <- apply(ams, 2, mean) hist(pest, prob=T) lines(density(pest)) abline(v=0.53, lwd=2) ## intervalos de confiança quantile(pest, prob=c(0.05, 0.95)) quantile(pest, prob=c(0.025, 0.975)) range(pest) ## agora estimando considerando a proporção p desconhecida am1 p1 <- mean(am1) p1 ## obtendo o intervalo de conviança p1 + qnorm(c(0.025, 0.975)) * sqrt(1/(4*2000)) ## margens de erro para diferentes tamanhos de amostra qnorm(c(0.025, 0.975)) * sqrt(1/(4*2000)) qnorm(c(0.025, 0.975)) * sqrt(1/(4*2100)) qnorm(c(0.025, 0.975)) * sqrt(1/(4*2200)) qnorm(c(0.025, 0.975)) * sqrt(1/(4*2300)) qnorm(c(0.025, 0.975)) * sqrt(1/(4*2400)) qnorm(c(0.025, 0.975)) * sqrt(1/(4*2500)) qnorm(c(0.025, 0.975)) * sqrt(1/(4*5000)) qnorm(c(0.025, 0.975)) * sqrt(1/(4*8000)) qnorm(c(0.025, 0.975)) * sqrt(1/(4*9000)) qnorm(c(0.025, 0.975)) * sqrt(1/(4*10000)) abs(qnorm(0.025)) ## tamanho da amostra para 95% de confiança e margem de erro 2% (1.96^2)/(4*0.02^2) ## tamanho da amostra para 95% de confiança e margem de erro 1% (1.96^2)/(4*0.01^2) abs(qnorm(0.005)) ## tamanho da amostra para 99% de confiança e margem de erro 2% (2.576^2)/(4*0.01^2)
Textos
Sobre a Fórmula de Sturges para a Construção de Histogramas
Distribuição de Poisson para o Número de Gols em Copas do Mundo
1)
Esta é uma listagem mínima de exercícios recomendados, entretanto todos os exercícios do Capítulo podem ser feitos
2)
Sugere-se aqui fazer também os exercícios de M.& L. Sec. 3.3: 1 a 6
3)
veja também seção 6.7 de B&M