Não foi possível enviar o arquivo. Será algum problema com as permissões?
Histórico do curso: CE-089 - 2o semestre de 2013
| Data | Conteúdo | Atividade | Tópico |
|---|---|---|---|
| 26/08 Seg (PJ) | Informações sobre o curso. Introdução à Edição de documentos científicos em LaTex. Fundamentos e funcionamento | Instalar o LaTeX, revisar o documento editado eu aula, alterar e editar seu próprio documento. | ver abaixo |
| 30/08 Sex (PJ) | Tópicos adicionais em edição em LaTeX. Tabelas, gráficos, formulas, referências | Produzir um texto em LaTeX sobre uma distribuição de probabilidades | ver abaixo |
| 02/09 Seg (PJ) | Introdução ao Sweave para editoração combinando LaTeX + R | Revisar o arquivo mostrado em aula, experimentando o processo de produção do documento e explorando alternativas. Iniciar um relatório de análise de algum conjunto de dados. | ver abaixo |
| 06/09 Sex (PJ) | Discussão sobre os relatórios apresentados com uso de LaTeX e/ou Sweave (LaTeX + R) | Produzir um texto editado com Sweave com um relatório de análise de dados | ver abaixo |
| 21/10 Seg (PJ) | Métodos numéricos em inferência por verossimilhança - revisão de conceitos, justificativas e algumas aplicações | ver abaixo | |
| 25/10 Sex (PJ) | Exemplos computacionais. Algoritmos para estimação, avaliação das funções e obtenção de intervalos | ver abaixo | |
| 28/10 Seg (PJ) | Recesso | ||
| 01/11 Sex (PJ) | Verossimilhança com dois parâmetros. Superfícies, verossimilhanças concentradas e perfis de verossimilhança. Parametrizações e ortogonalidade. Ex com distribuição Gamma | Refazer e complementar exercícios com distribuição Gama. Fazer para distribuição Beta (ou alguma outra com dois parâmetros) | ver abaixo |
| 04/11 Seg (PJ) | miscelânea de tópicos: precisão numérica, cálculos em modelos lineares, operações de matrizes, Cholesky e outras decomposições | ver abaixo | |
| 08/11 Sex | CONEST | ||
| 11/11 Seg (PJ) | Métodos de integração numérica: revisão - métodos baseados em aproximação do integrando, aproximação da integram e por amostragem. Aplicação em estimação por máxima verossimilhança de modelos de efeitos aleatórios | ver abaixo | |
| 15/11 Sex | Feriado | ||
| 18/11 Seg (PJ) | Aplicação em estimação por máxima verossimilhança de modelos de efeitos aleatórios | ver abaixo |
26/08
30/08
- Deve-se produzir (individualmente) um texto em LaTeX sobre alguma distribuição com elementos: listas, fórmulas, tabelas e gráficos.
- Informar os professores a distribuição escolhida (não deve haver duplicação)
- Lista dos alunos e distribuições escolhidas
| Acadêmico | Distribuição | Entrega |
|---|---|---|
| Bruno | F | recebido (04/09) |
| Daniel | Cauchy | recebido (06/09) |
| Eliane | Weibull | recebido (06/09) |
| Fillipe | COM-Poisson | recebido (06/09) |
| Karin | Gama | recebido (06/09) |
| Tiago | Binomial | recebido (06/09) |
| Vanessa | Gumbel | recebido (06/09) |
02/09
- Página do Sweave pelo seu desenvolvedor, F. Leisch
06/09
Produzir um texto (com editoração em Sweave) com um relatório de anáise de algum conjunto de dados
- O conjunto deve ser obtido pelo aluno a partir de dados disponíveis em alguma base com acesso público
- O relatório deve ter de 4-5 páginas e contar elementos de editoração e LaTeX (formulas, tabelas, gráficos, listas, capa, resumo, referências bibliográficas, citações cruzadase apêndice(s))
e uso do Sweave (para saidas inline e de chunks), incluindo tabelas (usar pacote xtable) e gráficos.
21/10
- Texto: Leitura/estudo recomendado - Cap. 1-3
- Atividades:
- Considere a seguinte amostra de uma distribuição
 com densidade
com densidade 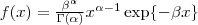
7,0 2,6 8,8 6,0 5,7 4,6 3,0 3,5 5,3 5,8 4,8 4,3
- Obtenha a expressão das funções de verossimilhança, log-verossimilhança, escore e hessiana
- Faça gráficos para cada uma dessas funções
- Escreva códigos para obtenção da estimativa de verossimilhança
- por maximização numérica
- por solução de sistema
- Obtenha um intervalos de confiança
- baseado na aproximação quadrática
- baseado na função de verossimilhança
- Seja a seguinte amostra de uma distribuição
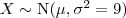
27 <25 22 20 [20-24] 22 26 23 >23 18 26 <32 22 23 >20
- resolva os mesmos itens da questão anterior
01/11
- Arquivo discutido em aula (atualizado em 05/11)
- Refazer os exemplos do arquivo, complementando para cada parametrização
- Montar/escrever o algoritmo Newton-Rapson para este problema
- Montar um material similar para a distribuição Beta
- Verificar possível(eis) (ao menos 1) reparametrização(ções)
- Verificar se é possível reduzir a dimensão do problema numérico (isolar 1 parâmetro)
- Montar soluções similares às do material da distribuição Gamma
04/11
- Miscelânea de tópicos (arquivo de comandos)
11/11
- Integração numérica (arquivo de comandos)
- Modelo de efeitos aleatórios (arquivo de comandos)