Tabela de conteúdos
José Cláudio Faria
Eu na Praia do Sul de Ilhéus/BA, em janeiro de 2007, refletindo profundamente sobre estatística computacional e o R!!!
Brincadeiras a parte…
1. Quem sou
- Engenheiro Agrônomo - Mestrado e Doutorado em Produção Vegetal pela Universidade Federal de Viçosa - UFV/MG - Pós-doc em estatística e experimentação agronômica (ESALQ)
2. O que tenho feito profissionalmente
- Professor de estatística e pesquisador da Universidade Estadual de Santa Cruz - UESC/BA;
- Tenho estado desenvolvendo algumas soluções computacionais voltadas para o ambiente R:
- Editores:
- Vim-R-plugin (http://www.vim.org/scripts/script.php?script_id=2628)
- Pacotes:
3. Sobre o R
- Gostaria de tê-lo encontrado desde o início de minha carreira na área de estatística computacional!
4. Sobre o futuro
- Desejo aprofundar os conhecimentos em análise multivariada de dados no ambiente R;
- Trocar experiências com pessoas e equipes envolvidas nestas áreas.
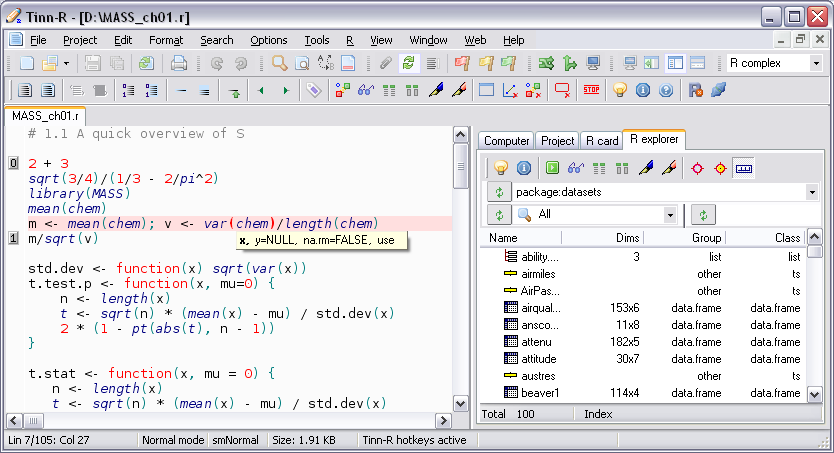
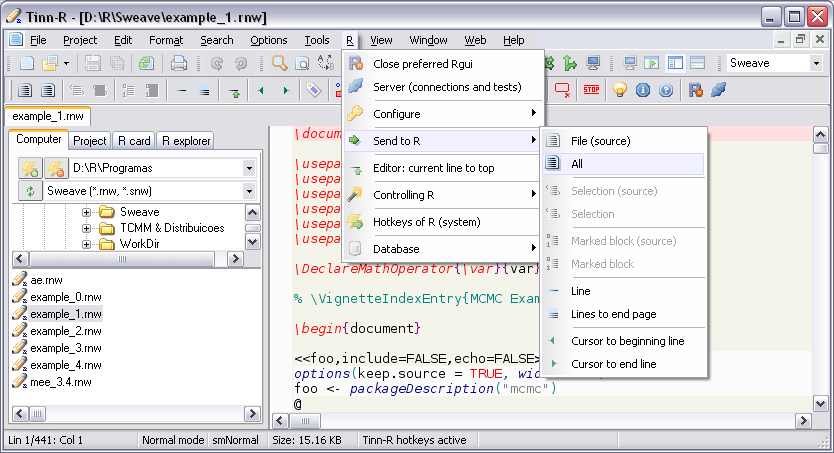
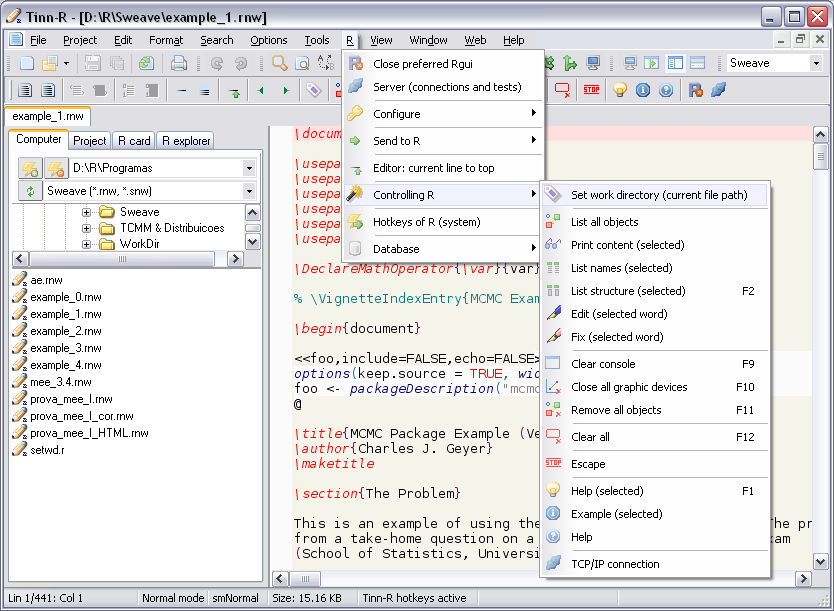
Tinn-R
Tinn-R GUI/Editor para o ambiente R sob Windows.
- O Tinn-R é um programa de código aberto (sob GPL) desenvolvido em Object Pascal com a IDE Delphi_7 da Borland;
- Facilita o uso do interpretador R e aumenta a produtividade das análises e documentações;
- Suporte ao Sweave;
- Permite interagir com o R em modo gráfico, o que aumenta a produtividade e facilita o uso, ao mesmo tempo em que estimula o aprendizado da linguagem R;
- Imagens:
Materiais sobre o R
Scripts
Todos os usuários estão automaticamente convidados a darem sugestões e alterarem contrutivamente todas as funções e scripts desta página. Solicito a gentileza de me enviar um email comunicando as alterações.
Introdução ao R
Abrir no Tinn-R e executar linha por linha buscando entender cada passo:
#===============================================================================
# Título: Introdução ao R - IR
# Curso : Métodos estatísticos aplicados à produção vegetal
# Autor : José Cláudio Faria/UESC/DCET
# Data : 15/12/06 18:39:16
# Versão: v7 - com comentários - cc
# Objetivos:
#===============================================================================
# a) Apresentar os recursos gráficos básicos do R
# b) Documentação e ajuda
# c) Funções elementares
# d) Estruturas de dados
# e) Operadores
# f) Estruturas de controle de fluxo
# g) Funções
#===============================================================================
#===============================================================================
# Exemplos
#===============================================================================
demo()
demo(package = .packages(all.available = TRUE))
demo(graphics) # Recursos gráficos genéricos
# Para teclar <Enter> to see next plot:
# é necessário que a tela esteja ativa
demo(image) # Recursos gráficos 2D
demo(persp) # Recursos gráficos 3D
library(lattice)
demo(lattice) # Recursos gráficos
demo(glm.vr) # Método lineares generalizados
demo(lm.glm) # Lineares e lineares generalizados
#===============================================================================
# Documentação e ajuda
#===============================================================================
?round
?'for' # ou ?”for“
?'[[' # ou ?”[[“
apropos('stem')
help.search('stem')
help.start() # ou menu 'Help/Html help
vignette() # documentos em pdf (dependente dos pacotes instalados)
vignette('grid') # abre pdf relacionado ao pacote grid
#===============================================================================
# Algumas funções elementares
#===============================================================================
set.seed(25)
x = round(runif(n = 20, min = 0, max = 10), digits = 2)
x
sort(x)
min(x)
max(x)
median(x) # mediana
mean(x) # média
var(x) # variância
sd(x) # desvio padrão (standard deviation)
sqrt(var(x))
sum(x) # somatório
length(x) # número de elementos
round(x, digits = 1)
round(x)
fivenum(x) # Returns Tukey's five number summary (minimum, lower-hinge, median, upper-hinge, maximum)
quantile(x) # quantis
quantile(x, c(0, .33, .66, 1))
cummax(x)
cummin(x)
plot(x, sin(x/20))
cor(x, sin(x/20))
# Imprimir no console uma mensagem ou o valor de uma variável:
print('Teste:')
x = 10
print(x)
# Concatenação:
cat('\nValor de x =', x); cat('\n')
cat('\n\tValor de x =', x); cat('\n')
#===============================================================================
# Estruturas de dados: MUITO IMPORTANTE!!!
#===============================================================================
#===============
# Vetores
#===============
# Algumas das diversas maneiras de defini-los:
c(1, 2, 3, 4, 5)
1:6
seq(1, 10, by = 1)
seq(1, 2, length = 10)
letters[1:5]
LETTERS[1:5]
# Algumas maneiras de recuperá-los:
x = seq(1, 10, by = 1)
x
x[5:10]
x[c(5, 7:10)]
x[-(5:10)]
x > 5
x[x > 5]
x[x < 6]
# Dar nomes aos componentes de um vetor:
names(x)
names(x) = letters[1:length(x)]
x
x['b']
c(a = 1, b = 5, c = 10)
# Algumas operações básicas:
set.seed(3)
x = round(runif(5, 0, 10), d = 1)
x
x/2
x*2
x+10
sort(x)
rev(sort(x))
set.seed(16)
x = sample(1:5, 10, replace = T)
x
sort(x)
unique(x)
x = c(1, 3, 2, 8, 5)
x
o = order(x)
o
x
x[o[1:3]]
#===============
# Matrizes
#===============
m = matrix(c(1, 2, 3, 4), nrow = 2)
m
m[1,2]
# O produto matricial:
x = matrix(c(6, 7), nrow = 2)
x
m %*% x
# O determinante de uma matriz:
det(m)
# A transposta de uma matriz:
t(m)
# Uma matriz diagonal:
diag(c(1,2))
# A identidade da matriz:
diag(1, 2)
diag(rep(1, 2))
diag(2)
# Comandos cbind e o rbind para criar matrizes:
cbind(c(1, 2), c(3, 4))
rbind(c(1, 3), c(2, 4))
# O traço de uma matriz:
sum(diag(m))
# A inversa de uma matriz :
solve(m)
solve(m, x)
solve(m) %*% x
# Autovalores:
eigen(m)$values
# Autovetores:
eigen(m)$vectors
# Certificar se a matriz é realmente diagonalisável:
p = eigen(m)$vectors
d = diag(eigen(m)$values)
p %*% d %*% solve(p)
#===============
# Arrays
#===============
ar = array(letters[1:24], c(2,4,3))
ar
ar[1,1,1] # ar[linha, coluna, dimensão] -> ar(x, y, z)
ar[1,1,2]
ar[1,2,3]
class(iris3)
iris3
#===============
# Fatores
#===============
set.seed(218)
x = factor(sample(c('a', 'b', 'c'), 5, replace = T))
x
l = c('d', 'e', 'f')
l
set.seed(17)
x = factor(sample(l, 5, replace = T), levels = l)
x
levels(x)
# Pode-se preferir uma tabela:
table(x)
# Se os valores estão de acordo com alguma razão, pode-se gerar níveis:
gl(1, 4)
gl(2, 4)
gl(2, 4, labels = c(T, F))
gl(2, 1, 8)
gl(2, 1, 8, labels = c(T, F))
# Pode fazer o produto cartesiano de dois fatores:
x = gl(2, 4)
x
y = gl(2, 1, length = 8)
y
interaction(x, y)
# O comando expand.grid é comparável (ele produz um frame), sendo muito útil para
# geração de níveis de fatores para as matrizes provenientes de dados
# experimentais:
a = c('a1', 'a2', 'a3')
b = c('b1', 'b2')
c = c('c1', 'c2')
dad = expand.grid(a, b, c)
names(dad) = c('A', 'B', 'C')
dad
#===============
# Frames
#===============
n = 10
set.seed(17)
dF = data.frame(x = rnorm(n),
y = sample(c(T, F), n, replace = T))
dF
# O comando str informa (retorna) a estrutura de um objeto e a parte dos dados
# que contém:
str(dF)
# Quando os objetos são armazenados, com sua própria ordem, o comando “unclass”
# da ordem pode alterá-lo:
n = 10
set.seed(3)
x = runif(n)
x
set.seed(19)
y = 1 - 2 * x + rnorm(n)
y
r = lm(y ~ x)
r
str(r)
r$coefficients
r$residuals
summary(r)
# A informação summary sumariza um objeto (aqui, um frame, mas vai bem com
# quase todos objetos):
summary(dF)
dF
# Pode-se ter acesso aos dados das colunas de diversas maneiras:
dF$x
dF[,1]
dF[['x']]
dim(dF)
names(dF)
row.names(dF)
# Ou pode-se mudar o nome das linhas ou das colunas:
names(dF) = c('a', 'b')
row.names(dF) = LETTERS[1:10]
names(dF)
row.names(dF)
str(dF)
# Pode-se ter acesso direto as colunas de um frame usando o comando attach().
# Obs: Não deve esquecer-se de destacá-lo detach() quando terminar:
data(faithful)
str(faithful)
attach(faithful)
str(eruptions)
detach()
#===============
# Listas
#===============
h = list()
h[['foo']] = 1
h[['bar']] = c('a', 'b', 'c')
str(h)
# Por exemplo, os parâmetros gráficos são armazenados em uma lista usada
# como contagens de chopping:
str(par())
h[['bar']] = NULL
str(h)
#===============
# Outros
#===============
# O comando split torna possível separar os dados de acordo com o valor
# de um fator:
n = 10
nn = 100
set.seed(21)
g = factor(round(n * runif(n * nn)))
x = rnorm(n * nn) + sqrt(as.numeric(g))
xg = split(x, g)
boxplot(xg, col = 'lavender', notch = TRUE, varwidth = TRUE)
str(xg)
# O comando apply torna possível aplicar uma função (para o exemplo, a média,
# quais, etc..) a cada coluna (ou linha) de um frame (ou de uma matriz):
options(digits = 4)
set.seed(5)
dF = data.frame(x = rnorm(20),
y = rnorm(20),
z = rnorm(20))
dF
apply(dF, 2, mean)
apply(dF, 2, range)
# Em dimensões mais elevadas:
options(digits=2)
set.seed(2)
m = array(rnorm(10^3), dim = c(10, 10, 10))
a = apply(m, 1, mean)
a
b = apply(m, c(1, 2), mean)
b
apply(b, 1, mean)
# A função tapply permite reagrupar as observações de acordo com o valor dos
# fatores e uma função (média, soma, etc..) para cada grupo obtido assim:
tapply(1:20, gl(2, 10, 20), sum)
by(1:20, gl(2, 10, 20), sum)
# A função sapply aplica a cada elemento de uma lista (ou de um vetor, etc..) e
# se possível retorna um vetor. A função lapply faz a mesma coisa, mas retorna
# uma lista:
x = list(a = rnorm(10),
b = runif(100),
c = rgamma(50, 1))
lapply(x, sd)
sapply(x, sd)
#===============================================================================
# Operadores
#===============================================================================
-5:7
set.seed(3)
x = floor(10*runif(10))
x
x[3]
x[1:3]
x[c(1, 2, 5)]
# O operador $ é reservado para recuperar um elemento de uma lista ou frame:
op = par()
op$col
op[['col']]
a = 'col'
op[[a]]
# A atribuição é feita por <- ou =.
x <- 1.17
x
y = c(1, 2, 3, 4)
y
# O produto de matrizes (% * %):
A = matrix(c(1, 2, 3, 4), nr = 2, nc = 2)
J = matrix(c(1, 0, 2, 1), nr = 2, nc = 2)
A
J
J %x% A
# O operador %o% é usado manufaturar tabelas da multiplicação
# (chama a função exterior com a multiplicação):
A = 1:5
B = 11:15
names(A) = A
names(B) = B
A %o% B
# A divisão euclidiana é %/%, seu restante é %%
1234 %% 3
1234 %/% 3
411*3 + 1
# A sociedade de uma 'unidade' é feita por %in%
17 %in% 1:100
17.1 %in% 1:100
# O operador ~ é usado descrever modelos (ANOVAS, métodos lineares, etc).
# Falaremos sobre ele mais tarde.
# Para mais detalhes (sobre os operadores negligenciados nestas notas)
# consulte o manual:
?'+'
?'<'
?'<-'
?'!'
?'['
?Syntax
?kronecker
?match
library(methods)
?slot
# Pode-se definir seus próprios operadores, pois são função diretas com dois
# argumentos cujo nome começa e as extremidades em %. O seguinte exemplo são
# tração do manual.
'%w/o%' = function(x, y) x[!x %in% y]
(1:10) %w/o% c(3,7,12)
#===============================================================================
# Estruturas de controle
#===============================================================================
set.seed(15)
x = rnorm(10)
x
y = ifelse(x > 0, 1, -1)
y
z = ifelse(x > 0, 1, ifelse(x < 0, '< zero', 0))
z
#===============
# Conexão:
#===============
set.seed(59)
x = letters[floor(1 + runif(1, 0, 4))]
x
y = switch(x,
a='Bonjour',
b='Gutten Tag',
c='Hello',
d='Konnichi wa')
y
#===============
# Loop for:
#===============
a = 0
for (i in 1:20) {
a = i
if(a <= 5 ) {
cat('a = ', a, '(<= 5)'); cat('\n')
next
}
if(a == 18) {
cat('a = ', a, '(= 18)'); cat('\n')
break
}
}
#===============
# Loop while:
#===============
a = 0
while (a < 11) {
if (a >= 3) print(a)
else cat('não\n')
a = a + 1 # expressão avaliada..
}
#===============
# Loop repeat:
#===============
a = 0
repeat {
a = a + 1
if (a >= 3) print(a)
else cat('não\n')
if (a == 10) break
}
#===============================================================================
# Funções
#===============================================================================
f = function(x) x/10 + 1
f(x = 10)
f(10) # Chamada alternativa
f = function(x) {
x/10 + 1
}
f(x = 10)
f(10) # Chamada alternativa
# Pode atribuir valores aos argumentos:
f = function(x, y = 3) {
x/10 + 1 - y
}
f(10)
# Na chamada da função, pode-se usar o nome dos argumentos, passar novos valores
# para as variáveis, não sendo necessário que os mesmos sigam a ordem declarada
# na função (desde que os valores sejam acompanhados dos respectivos nomes):
f(y = 1, x = 10)
f = function(x, y) {
x/10 + 1 - y
}
f(1, 10)
f(10, 1)
# No fim dos argumentos, pode haver três pontos, representando todos os
# argumentos não especificados:
f = function(x, ...) {
plot(x, ...)
}
Funções úteis
Superfície de resposta
Função plotlm3d
The simple, power and very flexible function plotlm3d enables you to plot 3d points and/or surfaces obtained from linear methods. It was adapted from scatter3d Rcmdr package of John Fox and some Deepayan Sarkar ideas.
It requires the rgl package that you can download from CRAN.
#===============================================================================
# Name : plotlm3d
# Original author: John Fox (scatter3d from package Rcmdr)
# Changes : Jose Claudio Faria and Duncan Murdoch
# Date (dd/mm/yy): 12/8/06 19:44:37
# Version : v18
# Aim : To plot 3d scatter, an or, surfaces with rgl package
#===============================================================================
# Arguments:
# x variable for horizontal axis.
# y variable for out-of-screen axis.
# z variable for vertical axis (response).
# surface plot surface(s) (TRUE or FALSE).
# model one or more linear model to fit ('z ~ x + y' is the default).
# groups if NULL (the default), no groups are defined; if a factor,
# a different surface or set of surfaces is plotted for each
# level of the factor; in this event, the colours in plane.col
# are used successively for the points and surfaces.
# model.by.group if TRUE the function will adjust one model for each level
# of groups; the order of the models must be the same of the
# level of the.
# model.summary print summary or summaries of the model(s) fit (TRUE or FALSE).
# simple.axes whether to draw sinple axes (TRUE or FALSE).
# box whether to draw a box (TRUE or FALSE).
# xlab,
# ylab,
# zlab axis labels.
# surface.col vector of colours for regression planes, used in the order
# specified by fit.
# point.col colour of points.
# grid.col colour of grid lines on the regression surface(s).
# grid plot grid lines on the regression surface(s) (TRUE or FALSE).
# grid.lines number of lines (default, 26) forming the grid, in each of
# the x and z directions.
# sphere.factor relative size factor of spheres representing points; the
# default size is dependent on the scale of observations.
# threshold if the actual size of the spheres is less than the threshold,
# points are plotted instead.
# speed revolutions of the plot per second.
# revolutions number of full revolutions of the display.
plotlm3d <- function (x, y, z,
surface = T,
model = 'z ~ x + y',
groups = NULL,
model.by.group = F,
model.summary = F,
simple.axes = T,
box = F,
xlab = deparse(substitute(x)),
ylab = deparse(substitute(y)),
zlab = deparse(substitute(z)),
surface.col = c('blue', 'orange', 'red', 'green',
'magenta', 'cyan', 'yellow', 'gray', 'brown'),
point.col = 'yellow',
grid.col = material3d("color"),
grid = T,
grid.lines = 26,
sphere.factor = 1,
threshold = 0.01,
speed = 0.5,
revolutions = 0)
{
require(rgl)
require(mgcv)
summaries <- list()
if ((!is.null(groups)) && model.by.group)
if (!nlevels(groups) == length(model))
stop('Model number is different of the number of groups')
if ((!is.null(groups)) && (nlevels(groups) > length(surface.col)))
stop('Number of groups exceeds number of colors')
if ((!is.null(groups)) && (!is.factor(groups)))
stop('groups variable must be a factor.')
xlab; ylab; zlab
valid <- if (is.null(groups))
complete.cases(x, y, z)
else
complete.cases(x, y, z, groups)
x <- x[valid]
y <- y[valid]
z <- z[valid]
if (!is.null(groups))
groups <- groups[valid]
levs <- levels(groups)
size <- max(c(x,y,z))/100 * sphere.factor
if (is.null(groups)) {
if (size > threshold)
spheres3d(x, y, z, color = point.col, radius = size)
else
points3d(x, y, z, color = point.col)
}
else {
if (size > threshold)
spheres3d(x, y, z, color = surface.col[as.numeric(groups)], radius = size)
else
points3d(x, y, z, color = surface.col[as.numeric(groups)])
}
aspect3d(c(1, 1, 1))
if (surface) {
xvals <- seq(min(x), max(x), length = grid.lines)
yvals <- seq(min(y), max(y), length = grid.lines)
dat <- expand.grid(x = xvals, y = yvals)
for (i in 1:length(model)) {
if (is.null(groups)) {
mod <- lm(formula(model[i]))
if (model.summary)
summaries[[model[i]]] <- summary(mod)
zhat <- matrix(predict(mod, newdata = dat), grid.lines, grid.lines)
surface3d(xvals, yvals, zhat, color = surface.col[i], alpha = 0.5, lit = F)
if (grid)
surface3d(xvals, yvals, zhat, color = grid.col, alpha = 0.5,
lit = F, front = 'lines', back = 'lines')
}
else { # groups is not NULL
if (!model.by.group) {
for (j in 1:length(levs)) {
mod <- lm(formula(model[i]), subset = (groups == levs[j]))
if (model.summary)
summaries[[paste(model[i], '.', levs[j], sep = '')]] <- summary(mod)
zhat <- matrix(predict(mod, newdata = dat), grid.lines, grid.lines)
surface3d(xvals, yvals, zhat, color = surface.col[j], alpha = 0.5, lit = F)
if (grid)
surface3d(xvals, yvals, zhat, color = grid.col, alpha = 0.5,
lit = F, front = 'lines', back = 'lines')
texts3d(min(x), min(y), predict(mod, newdata = data.frame(x = min(x), y = min(y),
groups = levs[j])), paste(levs[j], ' '), adj = 1, color = surface.col[j])
}
}
else { # model.by.group is TRUE
mod <- lm(formula(model[i]), subset = (groups == levs[i]))
if (model.summary)
summaries[[paste(model[i], '.', levs[i], sep = '')]] <- summary(mod)
zhat <- matrix(predict(mod, newdata = dat), grid.lines, grid.lines)
surface3d(xvals, yvals, zhat, color = surface.col[i], alpha = 0.5, lit = F)
if (grid)
surface3d(xvals, yvals, zhat, color = grid.col, alpha = 0.5,
lit = F, front = 'lines', back = 'lines')
texts3d(min(x), min(y), predict(mod, newdata = data.frame(x = min(x), y = min(y),
groups = levs[i])), paste(levs[i], ' '), adj = 1, color = surface.col[i])
}
}
}
}
if(simple.axes) {
axes3d(c('x', 'y', 'z'))
title3d(xlab = xlab, ylab = ylab, zlab = zlab)
}
else
decorate3d(xlab = xlab, ylab = ylab, zlab = zlab, box = box)
if (revolutions > 0) {
start <- proc.time()[3]
startMatrix <- par3d("userMatrix")
while ((theta <- speed*(proc.time()[3] - start))/2/pi < revolutions) {
rgl.viewpoint(userMatrix = rotate3d(startMatrix, theta, 0, 0, 1))
}
}
if (model.summary)
return(summaries)
else
return(invisible(NULL))
}
Usando a função plotlm3d
#===============================================================================
# Name : Script to test plotlm3d
# Author : Jose Claudio Faria and Duncan Murdoch
# Date (dd/mm/yy): 2012/07/01
# Version : v18
# Aim : To plot 3d scatter, an or, surfaces with rgl package
#===============================================================================
# mtrace(plotlm3d)
# mtrace.off
# Example 1
open3d()
rgl.bringtotop(stay = T)
with(iris, plotlm3d(Sepal.Length, Sepal.Width, Petal.Length,
surface = F,
groups = Species,
xlab = 'SL',
ylab = 'SW',
zlab = 'PL',
grid = F,
sphere.factor = 1))
# Example 2
open3d()
rgl.bringtotop(stay = T)
with(iris, plotlm3d(Sepal.Length,Sepal.Width, Petal.Length,
model = c('z ~ x + y',
'z ~ x + y + I(x^2) + I(y^2) + I(x*y)'),
surface = T,
groups = Species,
simple.axes = F,
box = T,
xlab = 'SL',
ylab = 'SW',
zlab = 'PL',
grid = F,
sphere.factor = 1))
# Example 3
open3d()
rgl.bringtotop(stay = T)
with(iris, plotlm3d(Sepal.Length,Sepal.Width, Petal.Length,
model = c('z ~ x + y',
'z ~ x + y + I(x^2) + I(y^2) + I(x*y)'),
surface = T,
xlab = 'SL',
ylab = 'SW',
zlab = 'PL',
grid = F,
sphere.factor = 1))
# Example 4
open3d()
rgl.bringtotop(stay = T)
with(iris, plotlm3d(Sepal.Length, Sepal.Width, Petal.Length,
model = c('z ~ x + y', # to setosa
'z ~ x + y + I(x^2) + I(y^2) + I(x*y)', # to versicolor
'z ~ I(x^3) + I(y^3)'), # to virginica
groups = Species,
model.by.group = T,
simple.axes = F,
box = F,
xlab = 'SL',
ylab = 'SW',
zlab = 'PL',
grid = F,
sphere.factor = 1))
# Example 5: Netter
x = c( 274, 180, 375, 205, 86, 265, 98, 330, 195, 53,
430, 372, 236, 157, 370)
y = c(2450, 3254, 3802, 2838, 2347, 3782, 3008, 2450, 2137, 2560,
4020, 4427, 2660, 2088, 2605)
z = c( 162, 120, 223, 131, 67, 169, 81, 192, 116, 55,
252, 232, 144, 103, 212)
mreg = lm(z ~ x + y)
ndata = data.frame(x = c(150, 274, 220, 370), y = c(4000, 2800, 3500, 3100))
zpred = predict(mreg, newdata = ndata, se.fit = F)
open3d()
rgl.bringtotop(stay = T)
plotlm3d(x, y, z,
surface = T,
model = 'z ~ x + y',
xlab = 'x',
ylab = 'y',
zlab = 'z')
spheres3d(x = c(150, 274, 220, 370), y = c(4000, 2800, 3500, 3100), zpred,
col = 'red', radius = 60)